1867

A note from Peter Guthrie Tait scribbled on an envelope asks an unknown recipient "Can't you come on Monday the present at the performance? An elliptical hole gives the rings in a state of vibration!!!"

In a room, thick with smoke, Tait and William Thomson (Lord Kelvin) are conducting an experiment to test the German physicist Hermann von Helmholtz's theory, that closed vortex lines in a fluid remain stable forever. Tait is using a box that emits smoke made from a pungent mixture of ammonia solution, salt and sulfuric acid. He taps the back of his makeshift vortex cannon, and thick rings he later describes as looking "like solid rings of India rubber" waft from a hole drilled in its front. Thomson develops a theory that each smoke ring is structured around knots in the ether, a space-filling substance believed to transmit matter. Consequently, Tait begins to tabulate possible forms of mathematical knots.

Klein worms

Klein worms are forms based on the klein bottle, drawn by the artist Claude Ponsot. These drawings made their first appearance as illustrations for the article Cybernetic Guerilla Warfare, by Paul Ryan (not the politician) in Radical Software, Vol.1, Issue 3.

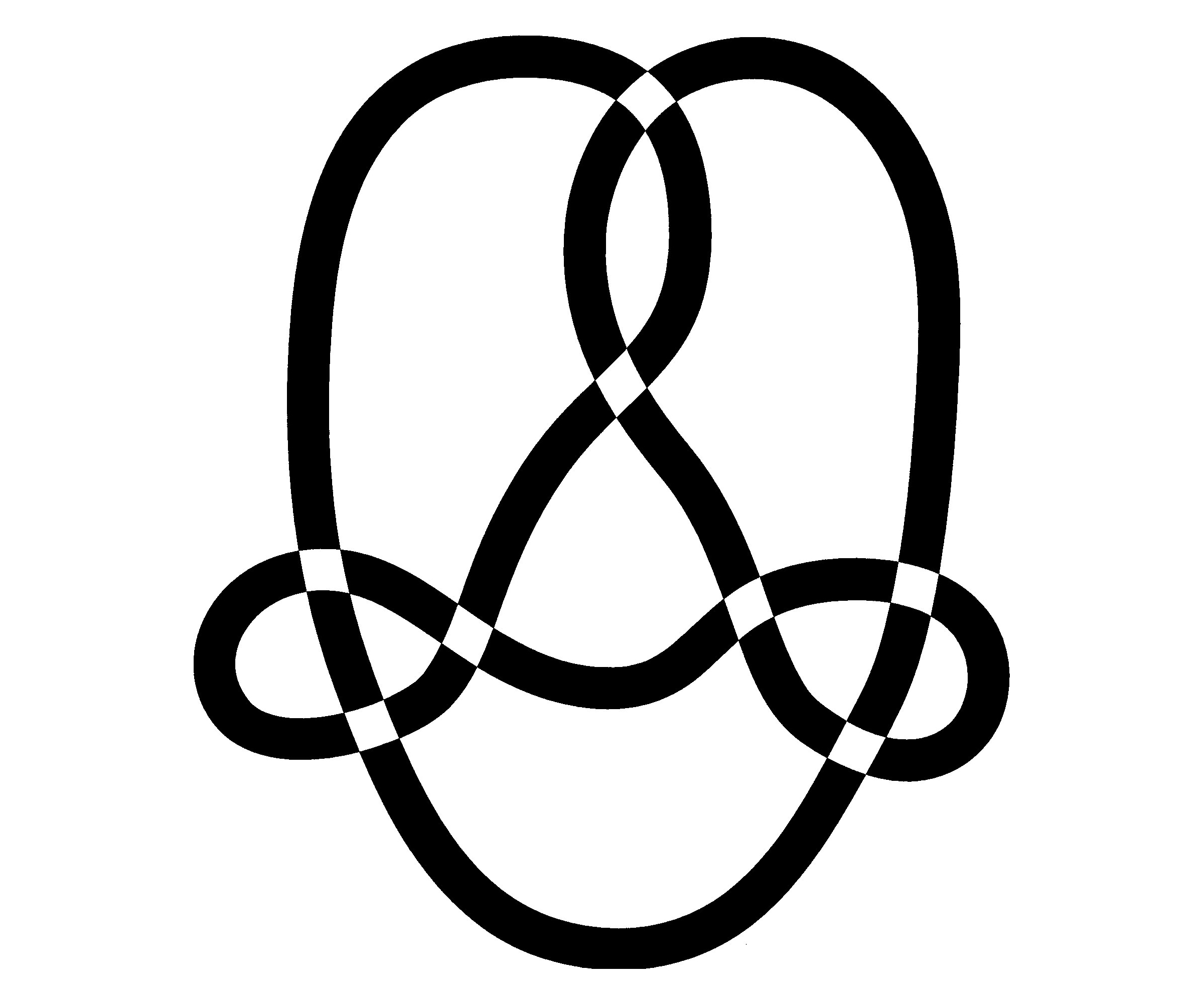
Knotworks

Knotworks are visualisations of the topology of our small, humble digital network of eight home servers. Each Knotwork drawing is of a mathematical knot with eight crossings, each crossing representing a node of the network. The points where the parts of the loop overlap can conceal parts contained, like the internal sections of klein worms. When unravelled, the knot is a continuous loop, and the links (edges) and the nodes (vertices) are the same.

Mathematical knots

Mathematical knots, or knots which are studied in the field of knot theory, are based on the embedding of a circle within three-dimensional space. They are different from the usual idea of a knot, that is a string with free ends. Therefore, mathematical knots are (almost) always considered to be closed loops.

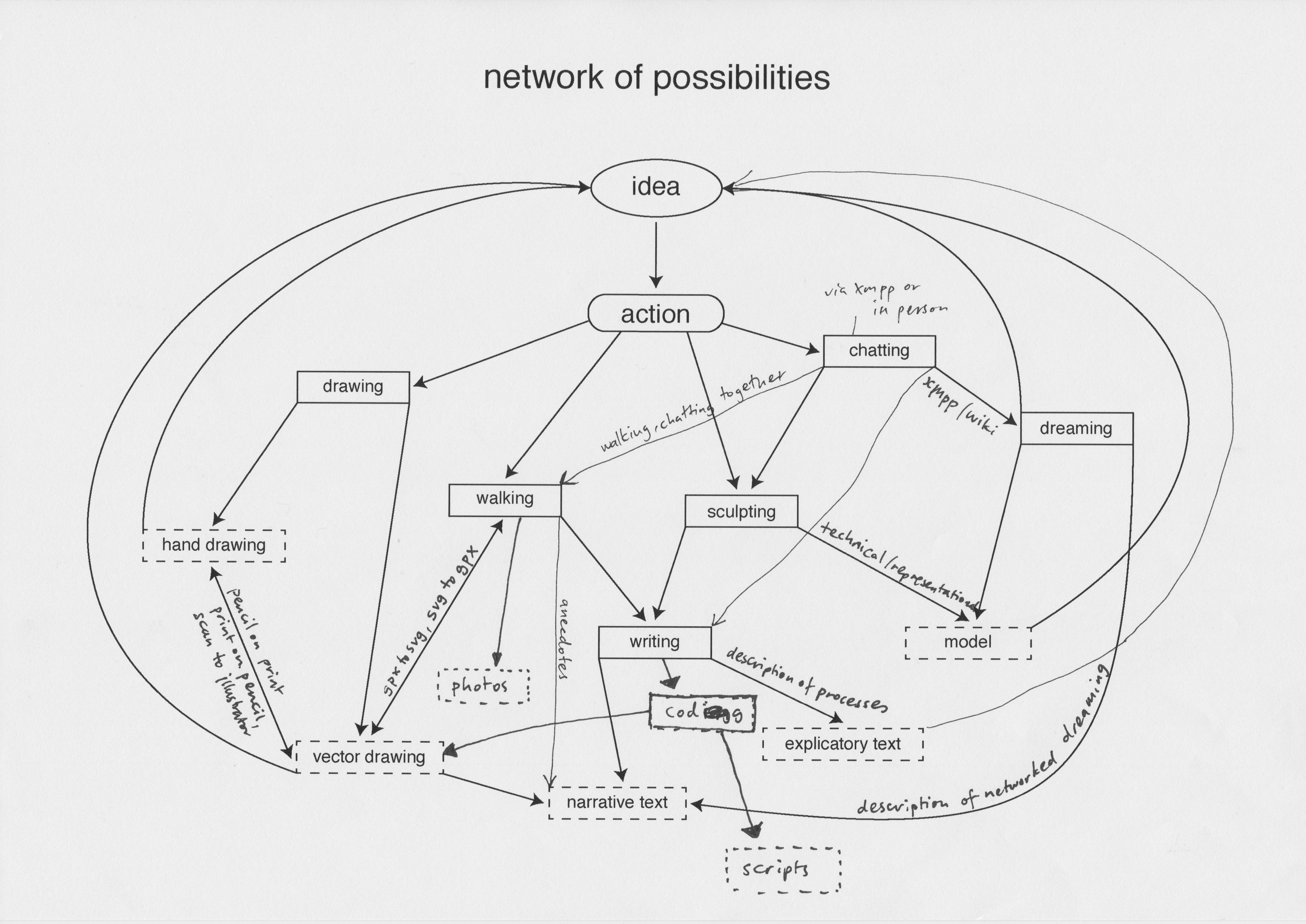
Network of possibilities

I'm making visualisations of things that are not visible in order to better understand them myself. The methodology I'm adopting is one based on a mind-map network, where possible ways to reflect are connected to subsequent actions and outcomes that infinitely loop into each other. In this way, an idea becomes an action (drawing, walking, sculpting, writing), which becomes an outcome (hand-drawing, GPS drawing, clay model, narrative text, explicatory text, and so on), then can become a new idea from which to act again, etcetera etcetera...

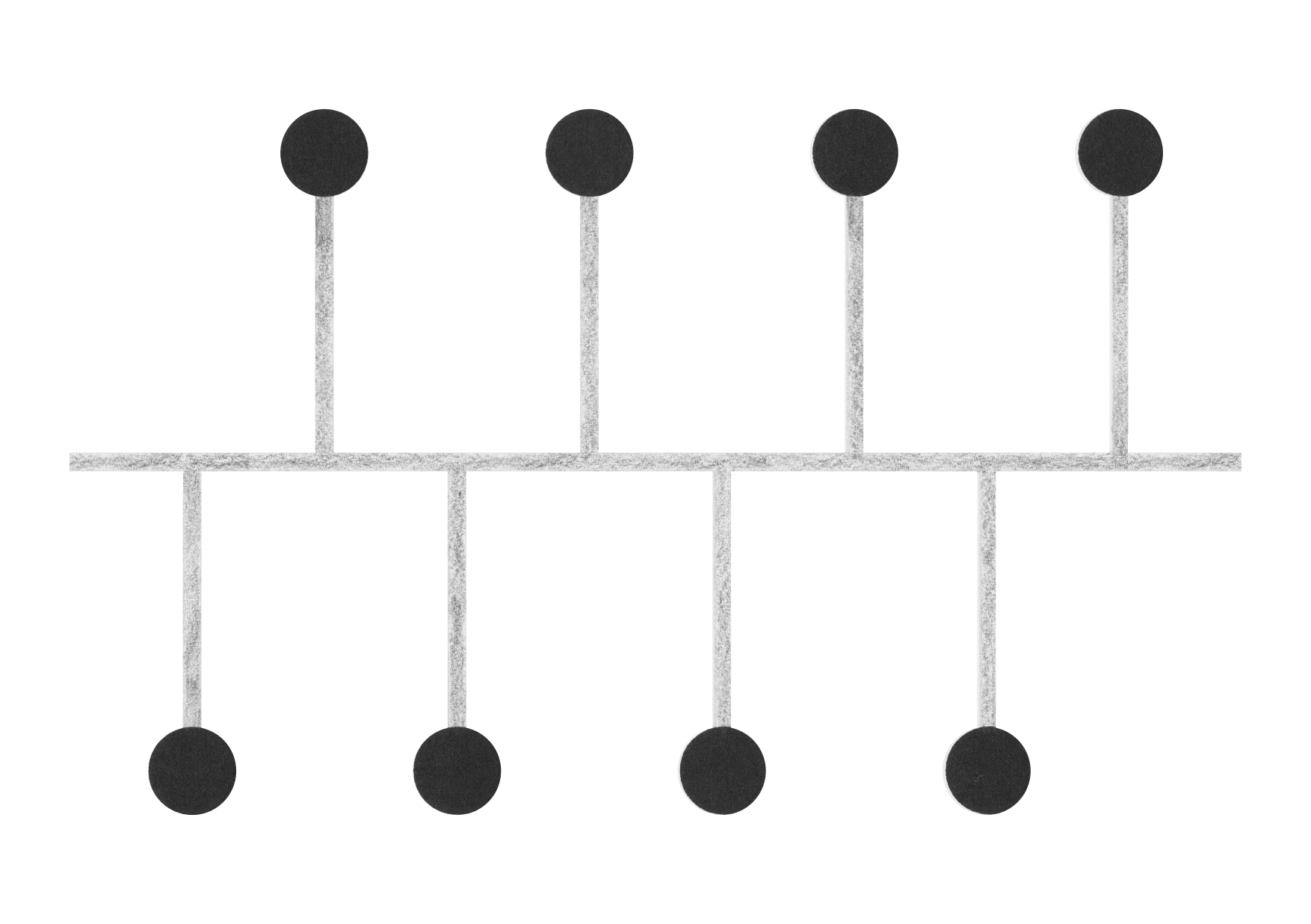
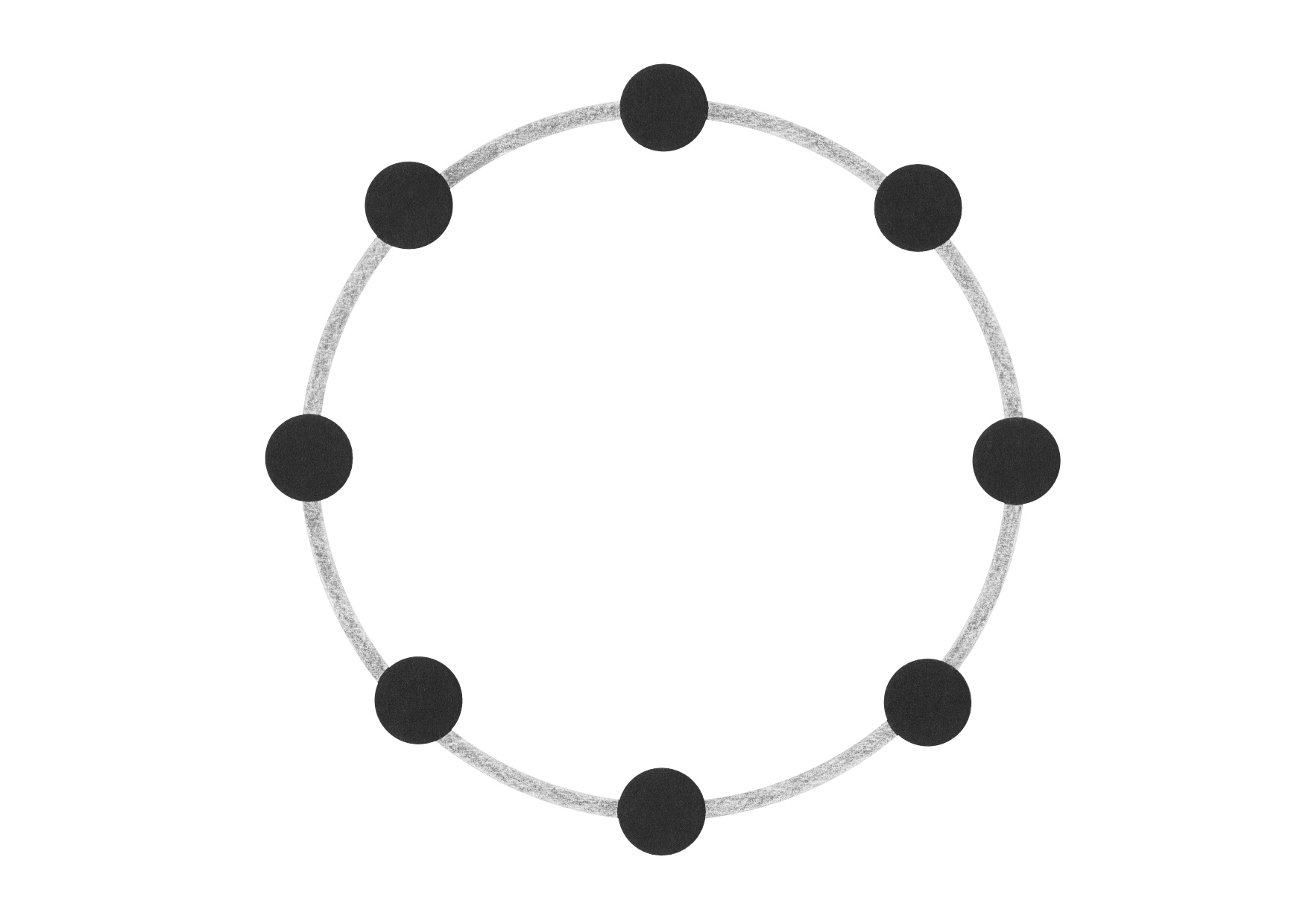
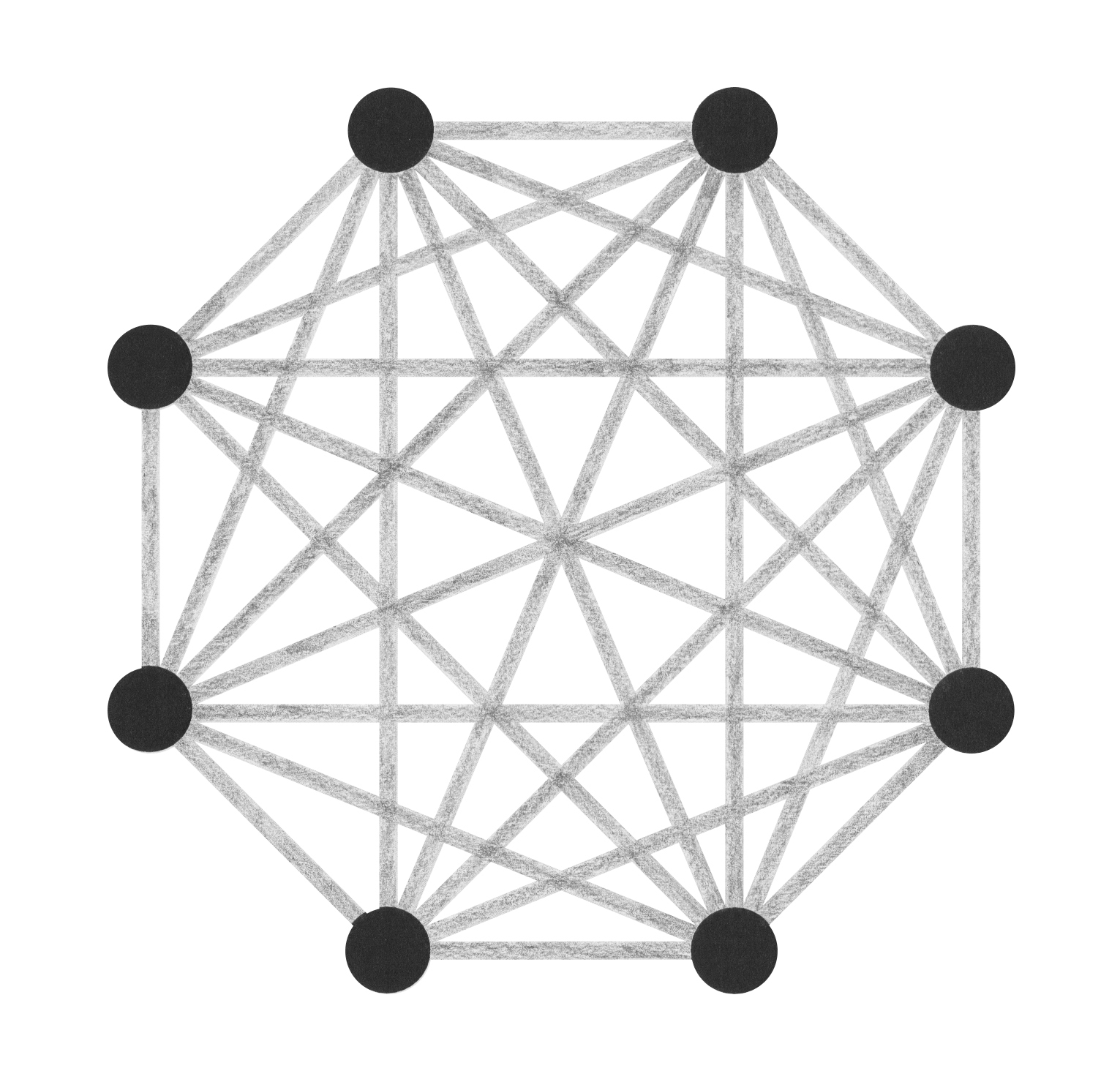
Network topology

Network topology is the arrangement of the elements (links, nodes, etc.) of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, including command and control radio networks, industrial fieldbusses, and computer networks.

There are two types of network topologies: physical and logical. Physical topology emphasizes the physical layout of the connected devices and nodes, while logical topology focuses on the pattern of data transfer between network nodes.