The Seven Bridges of Königsberg
The Seven Bridges of Königsberg is a historical mathematical problem which laid the ground for graph theory, and prefigured topology. Königsberg, in former Prussia (now Kaliningrad, Russia), set on both sides of the Pregel River, included two large islands - Kneiphof and Lomse - which were connected to the mainland by a series of seven bridges. The problem was to devise a walk through the city crossing each of those bridges once and only once.
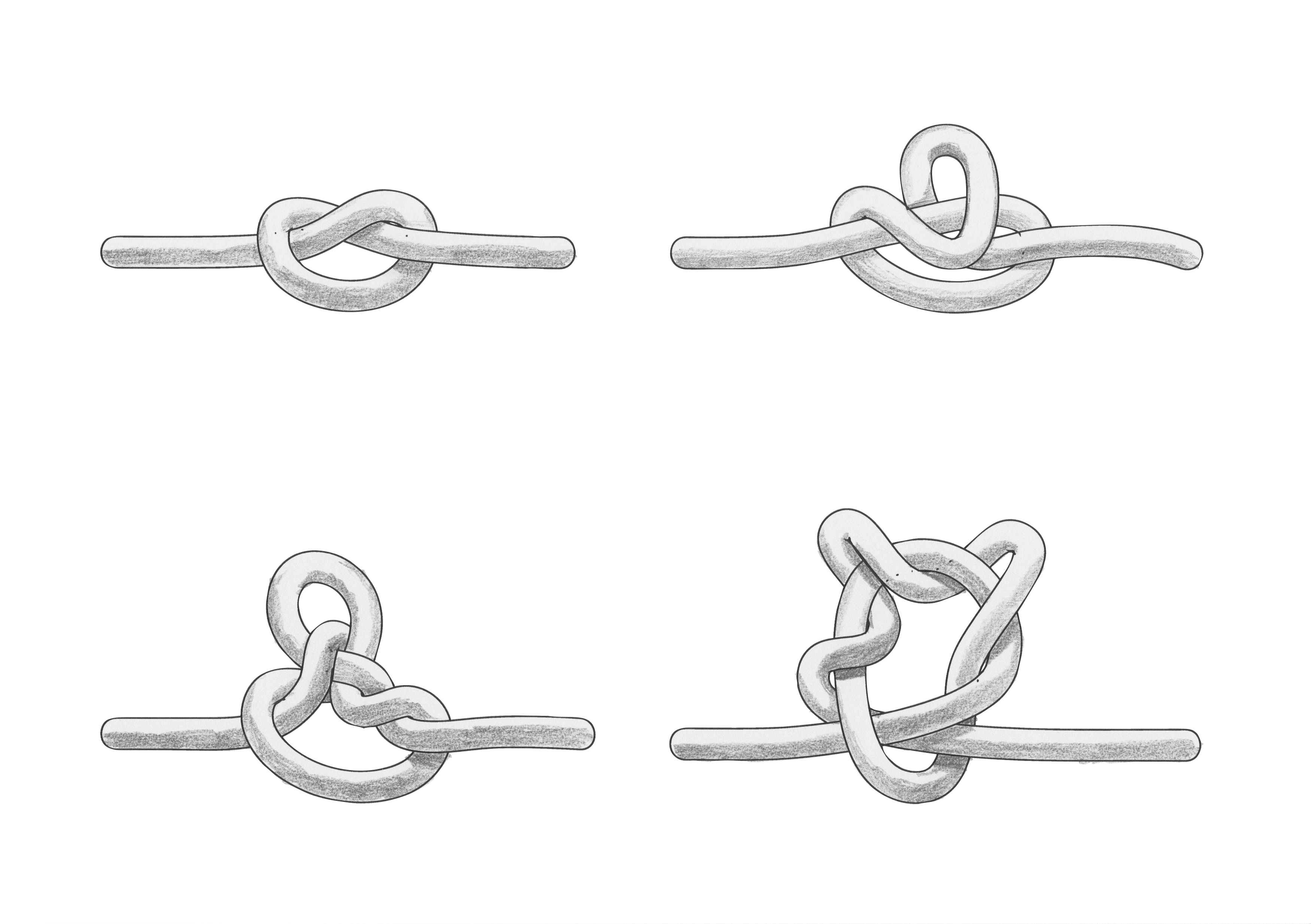
The negative solution came from Swiss mathematician and physicist Leonhard Euler, who pointed out that the choice of route inside each land mass was irrelevant; only the sequence of crossings mattered. Euler created a diagram in which each land mass was represented by a "vertex" or node, and each bridge became an "edge", or link between them. This allowed him to consider the problem in abstract terms, in the mathematical structure of a graph.
As only the connection information is relevant, the shape of the pictorial representations can be distorted in any way without changing the graph. For example, it does not matter if the links drawn are straight or curved, or whether a node is to the left or right of another.
Euler observed that, except at the beginning and end of the walk, if one enters a land mass by a bridge, one must leave a land mass by a bridge. In other words, at any time during the walk, the number of times one enters a non-terminal vertex equals the number of times one leaves it, meaning that the total number of bridges touching that land mass must be even, as half the crossings will be towards a land mass, and the other half away from it. However, all four of the land masses in the problem are touched by an odd number of bridges (one is touched by 5, the other three by 3). Since only two land masses can act as the beginning or end, it is impossible to cross each bridge only once during a walk.
Quipu
Quipu (also spelled khipu) or "talking knots", historically were cords with knots made in them as a way to record numbers, used by various ancient cultures of Andean South America.
Topology
In mathematics, topology is concerned with the properties of space that are preserved under continuous deformations, such as stretching, crumpling and bending, but not tearing or gluing.




Unraveling knots
The drawings I've been making by tracking myself over GPS makes a kind of map; however it does not display scale, or landmarks, or street names. It doesn't show which way is north, south, east or west. What it does show is some kind of graphic representation of the path I took by following my nose.
After I return back to the studio at Wijnhaven 61, I save and export .gpx (GPS exchange) format, and then drop the files into geographic information system software which allows me to accurately position the paths, representing them as lines.
Later, I export a line to .svg (scalable vector graphics) format and start to zoom in on it using a vector graphics editor. When zoomed out, the line appears to be curved, jagged, definitely not straight. However, when zooming in there are many straight lines, and they only bend at anchor points where each snapshot is taken. The line becomes knotted at places, representing social interactions, financial transactions, places where I backtracked, and where the GPS signal was obscured within or deflected by buildings in the urban landscape.
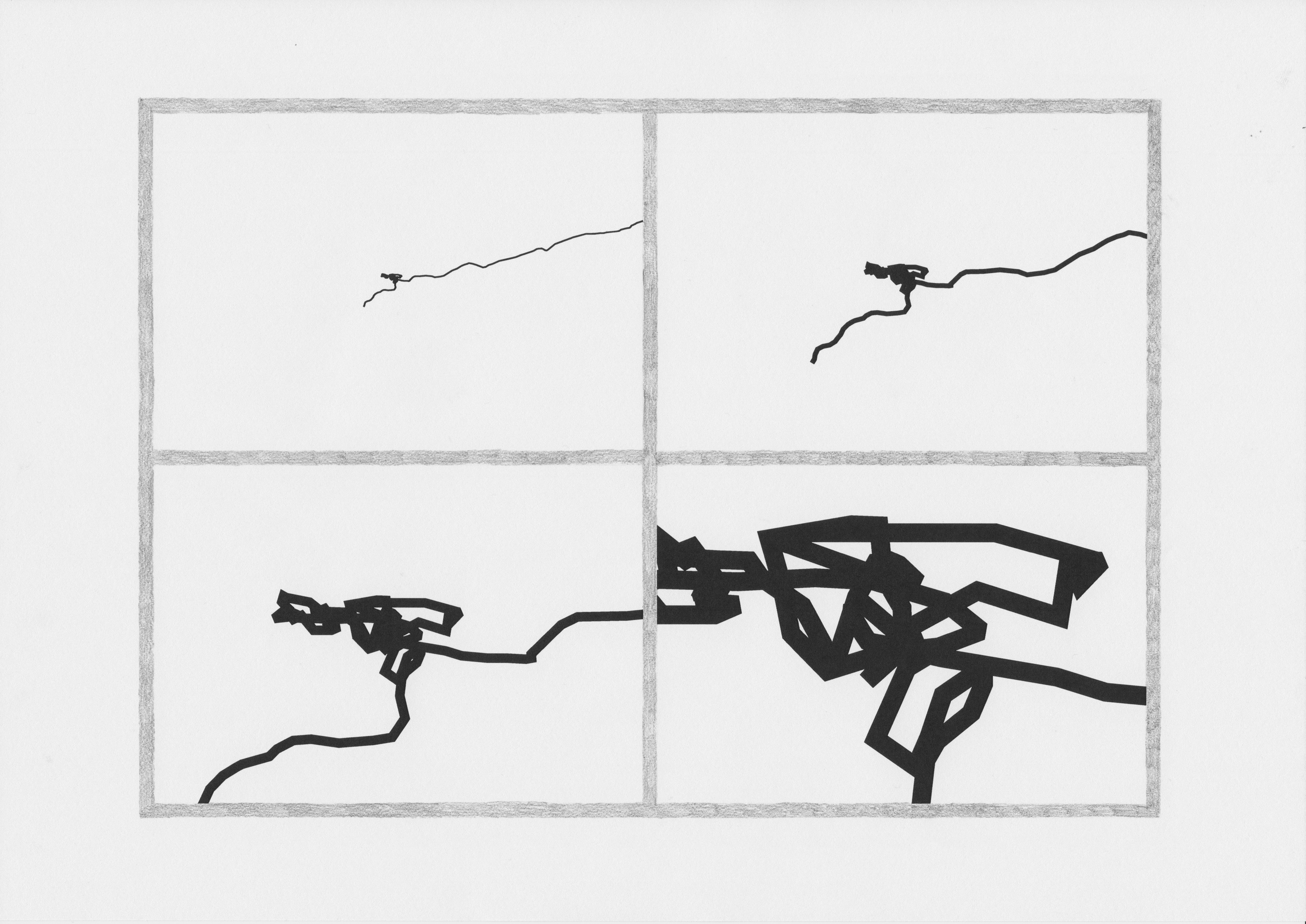
I begin to simplify the line, sliding a scale that removes anchor points and unravels the knot into a completely straight line. As I do this, I notice smaller knots that were not so visible at the scale I saw them at originally.


